Thursday, February 21, 2013
Saturday, February 9, 2013
Break from machine learning
France is currently quite cold. But I understand that we don't have nearly as much snow as you have in Ontario. We don't seem to have nearly as much time these days as we once did for some reason and it also gets dark very early and (as I said) it's pretty cold so I think for all of those reasons in some combined way we don't have as many photos to post as we once did and the original purpose of this blog was really to be a "photo blog" as Tom once suggested so that's too bad! But, I'm sure the photos will start coming back when it gets warmer and the days get longer and we (maybe) start having some more time somehow. In fact, this (the photo taking) might happen soon because we have a couple of friends coming at the end of the month and we'll likely do some kind of trip with them maybe to the South in search of some warmer temperatures (I think it's maybe 15 degrees in Marseille today)..
Unfortunately I got the response last night that our paper was not accepted to the WWW conference in May so I won't be going to Rio de Janeiro which is lamentable but life goes on I suppose. It's good work though (I think) but not fully developed yet and I think as we work on it and improve some things and get more results we'll get it at another conference (although in all likelihood it won't be as cool as the WWW conference and won't have as great of a location as Rio). Work is fine but moving along slowly as is usual it seems for me. I'm doing some work on "multi-task learning" which builds on the stuff being explained in the Grenoble Blog Tutorial Sets (TM) but here we try to improve our ability to learn by exploiting similarities in tasks. So for example let's say you're trying to classify patents into related/non-related to your area of interest but you only have 100 training examples and someone else wants to classify scientific papers into related/not-related to your area of interest but only has little training data as well. Well there's likely some latent features that are similar in each of the tasks and so even though they're not the same task if we learn them at the same time we can take advantage of the similarities between them and the extra training data from the other task. It is hard stuff in my opinion.
We have been training hard for our upcoming marathon in Annecy (the marathon is in Annecy, we haven't been training in Annecy). The training program that we're following calls for a lot of long runs (at least longer than what we've been used to during the week) and you know maybe that's part of where some of the time that we've been missing has gone. This week has been a bit of a "rest week" however which is nice and the kilometreage has been lower and we don't have to run very far tomorrow (Sunday) which is normally the big long run of the week. Therefore, we might actually take advantage of living in the mountains in winter time (we do so all the time in the summer time through biking) by doing some snow shoeing in the mountains tomorrow. The weather is supposed to be sunny but cold so hopefully we will go through with the plan! Another thing we signed up for a couple of days ago is the Grenoble-Vizille half-marathon. It's 2 weeks before our Annecy race so we need to be careful about going too fast but it should be a good "warm up" for the marathon and it's a really cool route following the famous "Route Napoléon". It's also neat because our running club (ASPA Meylan) is paying for our entry fee! What a nice group of people.
Ok so there are no new pictures (yet) but here are some old ones that you might recognize (I can't remember if I've put them here or somewhere or there or wherever before) and that will maybe help remind us that spring/summer is just around the corner...
Unfortunately I got the response last night that our paper was not accepted to the WWW conference in May so I won't be going to Rio de Janeiro which is lamentable but life goes on I suppose. It's good work though (I think) but not fully developed yet and I think as we work on it and improve some things and get more results we'll get it at another conference (although in all likelihood it won't be as cool as the WWW conference and won't have as great of a location as Rio). Work is fine but moving along slowly as is usual it seems for me. I'm doing some work on "multi-task learning" which builds on the stuff being explained in the Grenoble Blog Tutorial Sets (TM) but here we try to improve our ability to learn by exploiting similarities in tasks. So for example let's say you're trying to classify patents into related/non-related to your area of interest but you only have 100 training examples and someone else wants to classify scientific papers into related/not-related to your area of interest but only has little training data as well. Well there's likely some latent features that are similar in each of the tasks and so even though they're not the same task if we learn them at the same time we can take advantage of the similarities between them and the extra training data from the other task. It is hard stuff in my opinion.
We have been training hard for our upcoming marathon in Annecy (the marathon is in Annecy, we haven't been training in Annecy). The training program that we're following calls for a lot of long runs (at least longer than what we've been used to during the week) and you know maybe that's part of where some of the time that we've been missing has gone. This week has been a bit of a "rest week" however which is nice and the kilometreage has been lower and we don't have to run very far tomorrow (Sunday) which is normally the big long run of the week. Therefore, we might actually take advantage of living in the mountains in winter time (we do so all the time in the summer time through biking) by doing some snow shoeing in the mountains tomorrow. The weather is supposed to be sunny but cold so hopefully we will go through with the plan! Another thing we signed up for a couple of days ago is the Grenoble-Vizille half-marathon. It's 2 weeks before our Annecy race so we need to be careful about going too fast but it should be a good "warm up" for the marathon and it's a really cool route following the famous "Route Napoléon". It's also neat because our running club (ASPA Meylan) is paying for our entry fee! What a nice group of people.
Ok so there are no new pictures (yet) but here are some old ones that you might recognize (I can't remember if I've put them here or somewhere or there or wherever before) and that will maybe help remind us that spring/summer is just around the corner...
On the way down from l'Alpe d'Huez
Walking in Grenoble (Victor Hugo)
Warm warm warm times in Juan les Pins
Not as warm as above but still a lot warmer than right now in Avignon....
Sunday, February 3, 2013
Tutorial 2: More on regression
Hello students! I apologize if this is boring for some of you but I feel that it was so helpful to try to explain even the most basic things (because you realize that maybe you don't even understand it yourself when you're trying to explain it) so I will continue. Feel free (obviously) to skip if you're not at all interested and maybe next time I'll post some pictures of mountains or French cakes or something (stay tuned to this post however and you might be surprised! hey.. you can't just cheat and scroll down looking for the pictures right away.. that's not how this thing works.)
One thing you may be asking yourself is why do we need any math at all to predict y given x? We can easily plot the data and just predict a y value for any x by inspection. We could just take a look at the data and draw a line ourselves. Well, we started with a super easy example! Normally, we will have more than one feature. Consider whether a bank is going to accept a loan that you propose. The output y is YES or NO and the input x should generally consist of more than just the amount of the loan. They probably will want to consider the amount, your salary, your credit history, what the loan is for, etc. All of these are called.... that's right, features. Let's go back to those (grrrrr) cats. Say we still want to predict the weight of the brain, but now instead of just knowing the body weight, we also know the sex (seems reasonable, right?). We need a way for the computer to understand the feature 'sex' so let's just say that for a female cat, sex=1, and for a male cat, sex=2. Then, we can plot this data but we need a 3d plot now because the response (the brain weight) will be the on the vertical axis (the height), and the other two variables will be -- to be simple -- length and depth. It looks something like this:
So here the red points near the 'front' of the screen are female cats and the black points near the 'back' of the screen are males. We could still draw some kind of predictor but now it wouldn't just be a line, it would have to be a plane (like a flat rectangle). We can still learn this using our linear regression where the predictor will now be f(b,s) = h = w0 + w1*b + w2*s (I changed the function name from h to f because h is for the height in this problem and we don't want to get confused). So, given the body weight and the sex, we want to predict the height. When we run our gradient descent algorithm, we get the following learned parameters:
w0 = -0.4150
w1 = 4.0758
w2 = -0.0821
So, things are almost the same as before for the first two parameters, but the new parameter w2 shows that (because we chose s=1 for females and s=2 for males) we'll want to adjust down the estimate of the heart weight for males twice as much as we do for females. This also makes some intuitive sense because males may be bigger in general but we might expect heart weights to be more uniform. We can still graph the predictor (plane now) and it looks like this:
Note that this is not a great example because one of the axes (sex) is pretty limited in range (it's binary) but it helps to illustrate the point (I hope). If we had just one more feature then we could no longer visualize the data very easily and you start to see why we need computational approaches. Even with the single feature case although we could draw a line through the data that approximates the relationship, if we want to be precise and formal about things, getting the "best" fit can be done rigorously this way.
Ok, I'll give one more example that we can visualize (2 features) where there are more possibilities for the predictor features. Here, we want to predict the gas mileage (miles per gallon) of a car given its weight in tons and the horse power of the engine. Note that generally we would use even more features (for example maybe the number of cylinders in the engine) but we want to be able to visualize it for now just for our edification. Here's the data along with the predictor plane fit using our linear model:
Not bad, right? Here we can really see how you need a plane and how both features contribute to the overall prediction. For a little more "understanding" of what this provides us in terms of the features, here are the parameters for the weight and for the engine horse power:
weight = -3.87783
hp = -0.03177
So, we can see that the higher the weight, the lower the miles per gallon, and the higher the horse power, the lower the miles per gallon. Again, intuitive. We also see that since the weight parameter's magnitude is so much bigger, we can conclude that weight is a much more important factor than horse power in getting a lower mpg.
When we're performing much more complex regression with many (maybe hundreds or even thousands) of features, of course there's no way that we can visualize it perfectly. But, we can determine a predictor function and a lot of the time do quite well.
One other thing you may be wondering about is why we have to use an incremental approach to learn the parameters. Well, in most interesting applications, we do have to, but here we actually don't (I just showed it because it's the more general approach). It turns out that for this simple problem we can get a closed-form (exact) solution without having to incrementally get there. I won't go through the math now, but for simple linear regression, if all of our training data is stored in a matrix X where each row is a training example and each column represents a single feature, then we can get the exact values for the parameters (the w's) as follows:
w = (XTX)-1XTy
Cool, eh?
Perhaps next time we'll look at either binary classification (perhaps given the body and heart weight of the cat, predict its sex) and maybe we'll cover some more goods on linear regression! EXCITEMENT AWAITS!!!
One thing you may be asking yourself is why do we need any math at all to predict y given x? We can easily plot the data and just predict a y value for any x by inspection. We could just take a look at the data and draw a line ourselves. Well, we started with a super easy example! Normally, we will have more than one feature. Consider whether a bank is going to accept a loan that you propose. The output y is YES or NO and the input x should generally consist of more than just the amount of the loan. They probably will want to consider the amount, your salary, your credit history, what the loan is for, etc. All of these are called.... that's right, features. Let's go back to those (grrrrr) cats. Say we still want to predict the weight of the brain, but now instead of just knowing the body weight, we also know the sex (seems reasonable, right?). We need a way for the computer to understand the feature 'sex' so let's just say that for a female cat, sex=1, and for a male cat, sex=2. Then, we can plot this data but we need a 3d plot now because the response (the brain weight) will be the on the vertical axis (the height), and the other two variables will be -- to be simple -- length and depth. It looks something like this:
So here the red points near the 'front' of the screen are female cats and the black points near the 'back' of the screen are males. We could still draw some kind of predictor but now it wouldn't just be a line, it would have to be a plane (like a flat rectangle). We can still learn this using our linear regression where the predictor will now be f(b,s) = h = w0 + w1*b + w2*s (I changed the function name from h to f because h is for the height in this problem and we don't want to get confused). So, given the body weight and the sex, we want to predict the height. When we run our gradient descent algorithm, we get the following learned parameters:
w0 = -0.4150
w1 = 4.0758
w2 = -0.0821
So, things are almost the same as before for the first two parameters, but the new parameter w2 shows that (because we chose s=1 for females and s=2 for males) we'll want to adjust down the estimate of the heart weight for males twice as much as we do for females. This also makes some intuitive sense because males may be bigger in general but we might expect heart weights to be more uniform. We can still graph the predictor (plane now) and it looks like this:
Note that this is not a great example because one of the axes (sex) is pretty limited in range (it's binary) but it helps to illustrate the point (I hope). If we had just one more feature then we could no longer visualize the data very easily and you start to see why we need computational approaches. Even with the single feature case although we could draw a line through the data that approximates the relationship, if we want to be precise and formal about things, getting the "best" fit can be done rigorously this way.
Ok, I'll give one more example that we can visualize (2 features) where there are more possibilities for the predictor features. Here, we want to predict the gas mileage (miles per gallon) of a car given its weight in tons and the horse power of the engine. Note that generally we would use even more features (for example maybe the number of cylinders in the engine) but we want to be able to visualize it for now just for our edification. Here's the data along with the predictor plane fit using our linear model:
Not bad, right? Here we can really see how you need a plane and how both features contribute to the overall prediction. For a little more "understanding" of what this provides us in terms of the features, here are the parameters for the weight and for the engine horse power:
weight = -3.87783
hp = -0.03177
So, we can see that the higher the weight, the lower the miles per gallon, and the higher the horse power, the lower the miles per gallon. Again, intuitive. We also see that since the weight parameter's magnitude is so much bigger, we can conclude that weight is a much more important factor than horse power in getting a lower mpg.
When we're performing much more complex regression with many (maybe hundreds or even thousands) of features, of course there's no way that we can visualize it perfectly. But, we can determine a predictor function and a lot of the time do quite well.
One other thing you may be wondering about is why we have to use an incremental approach to learn the parameters. Well, in most interesting applications, we do have to, but here we actually don't (I just showed it because it's the more general approach). It turns out that for this simple problem we can get a closed-form (exact) solution without having to incrementally get there. I won't go through the math now, but for simple linear regression, if all of our training data is stored in a matrix X where each row is a training example and each column represents a single feature, then we can get the exact values for the parameters (the w's) as follows:
w = (XTX)-1XTy
Cool, eh?
Perhaps next time we'll look at either binary classification (perhaps given the body and heart weight of the cat, predict its sex) and maybe we'll cover some more goods on linear regression! EXCITEMENT AWAITS!!!
Saturday, February 2, 2013
Tutorial 1: Explaining Life at Xerox
In the first of a series of tutorials (some of which may be contributed by guest bloggers), the Grenoble Blog (TM) will explain how to explain life at Xerox in the specific case of the author. In other tutorials -- coming soon -- we hope to cover a wide spectrum of topics ranging from (Dei Gratia Regina) firearm assembly/disassembly to watch repair (we reserve the right to alter what topics will ultimately be covered).
In the valley of the alps in South-Eastern France, the Chateau Maupertuis houses the Xerox Research Centre Europe (XRCE). It is here that the author stumbles through the ups and downs of a life led in the pursuit of a better world for all (except cats). Because Romans chapter 12 verse 16 tells us to "... not be proud, but be willing to associate with people of low position", we study machine learning so that we may one day replace the people of low position with machines.
In my infinitely high view of myself, I imagine that in your daily lives you are constantly attempting to explain to your friends and colleagues what it is that I, the author, does at such a place as XRCE (because they are no doubt asking you!). To make life easier for you (the core mantra at our centre), and because docendo disco, scribendo cogito, I will proceed to attempt to explain some of the basics of one of the areas of study that I subscribe to, which is -- as noted above -- the field of machine learning (ML).
The most concise definition of the area is that ML consists of creating machines (systems, software, whatever) that can learn from data (makes sense, no?). Wow it's a huge subject. There's probably at least 70 jillion papers that fall under this area so where does one begin? Well, how about supervised learning? Here, the goal is to create a system that can predict future outcomes based on learning by example and then generalizing. At its simplest, this is basic regression.
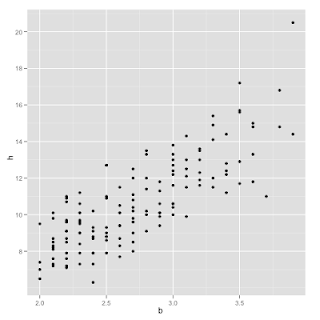
Say we have a bunch of data pairs (x,y) where x is the body weight of a domestic cat in kg and y is the weight of its heart in grams (gah! cats!!!!). By giving our system a bunch of these examples, we want it to generalize (learn) from what it sees and then be able to predict the expected weight of its heart given its body weight. So, we want to learn a function h(x) such that when we input some x (body weight) it outputs some y (heart weight). The data looks like this:
So, it looks like the relationship between body weight (along the horizontal axis) and heart weight (the vertical axis) is linear. That is, we should be able to use a linear function to predict heart weight given body weight. Because the relationship seems to be linear, we can say that our predictor h(x) = xTw = sum over the components in x times the components in w where w is a vector of parameters (this is what the algorithm will learn).
For complex machine learning problems, one of the most important issues is representation. We need a way to represent the data in a way that the computer can understand it and the data from this representation that are used to learn are called features. For this simple problem, there is only a single feature: the body weight of the (most likely evil) cat. For applications such as text classification, where we want to classify documents into categories, the features are often "bags of words". This means that each document is represented as counts of words. The short document "Hello how are you doing? I am doing fine." would be represented as follows:
Hello:1, how:1, are:1, you:1, doing:2, I:1, am:1, fine:1.
In this representation, the size of the feature space is the total number of words in the vocabulary.
Back to the simple problem above, although there is only a single feature, we also always add an 'imaginary' feature that is equal to 1 so that the learned predictor line can have an intercept other than 0; this is called the bias. So, we have x0*w0 + x1*w1 = y where x0 = 1 and we want to learn w = (w0, w1) from the data.
Since we have some existing example (or "training") data, we know that our function that we learn, for each x, should be close to its corresponding y. To do this, we need to decide on some loss function that we want to minimize over the training data. There are many of these and they have reasons for being chosen but for now we'll choose the following:
L(w) = (1/2) sum over all training examples (x(i)Tw - y(i))2 where the (i) superscripts denote each of the training examples that we have. This is called the least squares loss function because we are going to minimize (with respect to the parameters) the squared error between our prediction and the correct answer for each of the training examples.
So, how do we minimize the loss with respect to w? If you remember basic calculus, you know that if you take the derivative of a function you will get -- in a sense -- the "direction" it's going and you can follow that direction until you reach the minimum. So, this is called the gradient descent algorithm because you're descending to the minimum by following the gradient. We learn the weights iteratively by going through the data and adjusting them in the direction of the gradient as follows:
wj ← wj + η (d/dw)L(w)
where η is the learning rate. It decides how far we go with each step towards the minimum. If this is too big then we might go to far, passing the minimum on each step, and never arriving. If it's too small, it might take forever to get there because we're only getting infinitesimally closer each time.
So, what is the partial derivative of the loss function L(w) with respect to w? It turns out to be: (y(i) - x(i)Tw)x(i). So our final update in passing through the data is:
wj ← wj + η (y(i) - x(i)Tw)x(i)
This makes intuitive sense. Each time we look at an example and a feature, we alter the parameter by the amount that it was wrong. If y (the correct answer) was 5 and our prediction (x(i)Tw) was 10, then we predicted too much and the amount in the brackets will be -5. We will therefore decrement that parameter proportionally to -5. If they are very close, then we only need to make a very small update. If they are the exact same, then the update is 0 because we're at a perfect value.
There are different ways to perform these updates but one of them is called stochastic gradient descent and in this version we make updates to each of the parameter values one at a time for each datapoint. This has advantages for very large datasets (one problem is that you would never reach a perfect minimum if you don't employ a decreasing step size -- you would just jump around the minimum.. but for many problems even with a static step size you can do quite well).
Running this algorithm, we get the following parameter values:
w0 = -0.3567
w1 = 4.0341
That means, if we had a cat with body weight x=2.6kg, we would predict a heart weight of y = h(2.6) = -0.3567 + (2.6)(4.0341) = 10.13196 g. Here is that point (red) and the general predictor (blue) shown with the original training data:
Ta-da! Isn't that grand?
I was going to cover binary classification next (given some input x, predict whether it fits in the class NO (y=-1) or YES (y=1) where a common real-world example [where the e-mails are represented with the bag-of-words representation] is to tag e-mails as either SPAM or NOT-SPAM) but (believe it or not) this thing took me all afternoon on a Saturday. Maybe next time!!!
I'll leave you with a picture of my favourite twin-city of St. Donat, Quebec, Lans-en-Vercors:
XRCE
In the valley of the alps in South-Eastern France, the Chateau Maupertuis houses the Xerox Research Centre Europe (XRCE). It is here that the author stumbles through the ups and downs of a life led in the pursuit of a better world for all (except cats). Because Romans chapter 12 verse 16 tells us to "... not be proud, but be willing to associate with people of low position", we study machine learning so that we may one day replace the people of low position with machines.
In my infinitely high view of myself, I imagine that in your daily lives you are constantly attempting to explain to your friends and colleagues what it is that I, the author, does at such a place as XRCE (because they are no doubt asking you!). To make life easier for you (the core mantra at our centre), and because docendo disco, scribendo cogito, I will proceed to attempt to explain some of the basics of one of the areas of study that I subscribe to, which is -- as noted above -- the field of machine learning (ML).
The most concise definition of the area is that ML consists of creating machines (systems, software, whatever) that can learn from data (makes sense, no?). Wow it's a huge subject. There's probably at least 70 jillion papers that fall under this area so where does one begin? Well, how about supervised learning? Here, the goal is to create a system that can predict future outcomes based on learning by example and then generalizing. At its simplest, this is basic regression.
Say we have a bunch of data pairs (x,y) where x is the body weight of a domestic cat in kg and y is the weight of its heart in grams (gah! cats!!!!). By giving our system a bunch of these examples, we want it to generalize (learn) from what it sees and then be able to predict the expected weight of its heart given its body weight. So, we want to learn a function h(x) such that when we input some x (body weight) it outputs some y (heart weight). The data looks like this:
So, it looks like the relationship between body weight (along the horizontal axis) and heart weight (the vertical axis) is linear. That is, we should be able to use a linear function to predict heart weight given body weight. Because the relationship seems to be linear, we can say that our predictor h(x) = xTw = sum over the components in x times the components in w where w is a vector of parameters (this is what the algorithm will learn).
For complex machine learning problems, one of the most important issues is representation. We need a way to represent the data in a way that the computer can understand it and the data from this representation that are used to learn are called features. For this simple problem, there is only a single feature: the body weight of the (most likely evil) cat. For applications such as text classification, where we want to classify documents into categories, the features are often "bags of words". This means that each document is represented as counts of words. The short document "Hello how are you doing? I am doing fine." would be represented as follows:
Hello:1, how:1, are:1, you:1, doing:2, I:1, am:1, fine:1.
In this representation, the size of the feature space is the total number of words in the vocabulary.
Back to the simple problem above, although there is only a single feature, we also always add an 'imaginary' feature that is equal to 1 so that the learned predictor line can have an intercept other than 0; this is called the bias. So, we have x0*w0 + x1*w1 = y where x0 = 1 and we want to learn w = (w0, w1) from the data.
Since we have some existing example (or "training") data, we know that our function that we learn, for each x, should be close to its corresponding y. To do this, we need to decide on some loss function that we want to minimize over the training data. There are many of these and they have reasons for being chosen but for now we'll choose the following:
L(w) = (1/2) sum over all training examples (x(i)Tw - y(i))2 where the (i) superscripts denote each of the training examples that we have. This is called the least squares loss function because we are going to minimize (with respect to the parameters) the squared error between our prediction and the correct answer for each of the training examples.
So, how do we minimize the loss with respect to w? If you remember basic calculus, you know that if you take the derivative of a function you will get -- in a sense -- the "direction" it's going and you can follow that direction until you reach the minimum. So, this is called the gradient descent algorithm because you're descending to the minimum by following the gradient. We learn the weights iteratively by going through the data and adjusting them in the direction of the gradient as follows:
wj ← wj + η (d/dw)L(w)
where η is the learning rate. It decides how far we go with each step towards the minimum. If this is too big then we might go to far, passing the minimum on each step, and never arriving. If it's too small, it might take forever to get there because we're only getting infinitesimally closer each time.
So, what is the partial derivative of the loss function L(w) with respect to w? It turns out to be: (y(i) - x(i)Tw)x(i). So our final update in passing through the data is:
wj ← wj + η (y(i) - x(i)Tw)x(i)
This makes intuitive sense. Each time we look at an example and a feature, we alter the parameter by the amount that it was wrong. If y (the correct answer) was 5 and our prediction (x(i)Tw) was 10, then we predicted too much and the amount in the brackets will be -5. We will therefore decrement that parameter proportionally to -5. If they are very close, then we only need to make a very small update. If they are the exact same, then the update is 0 because we're at a perfect value.
There are different ways to perform these updates but one of them is called stochastic gradient descent and in this version we make updates to each of the parameter values one at a time for each datapoint. This has advantages for very large datasets (one problem is that you would never reach a perfect minimum if you don't employ a decreasing step size -- you would just jump around the minimum.. but for many problems even with a static step size you can do quite well).
Running this algorithm, we get the following parameter values:
w0 = -0.3567
w1 = 4.0341
That means, if we had a cat with body weight x=2.6kg, we would predict a heart weight of y = h(2.6) = -0.3567 + (2.6)(4.0341) = 10.13196 g. Here is that point (red) and the general predictor (blue) shown with the original training data:
Ta-da! Isn't that grand?
I was going to cover binary classification next (given some input x, predict whether it fits in the class NO (y=-1) or YES (y=1) where a common real-world example [where the e-mails are represented with the bag-of-words representation] is to tag e-mails as either SPAM or NOT-SPAM) but (believe it or not) this thing took me all afternoon on a Saturday. Maybe next time!!!
I'll leave you with a picture of my favourite twin-city of St. Donat, Quebec, Lans-en-Vercors:
Subscribe to:
Comments (Atom)