XRCE
In the valley of the alps in South-Eastern France, the Chateau Maupertuis houses the Xerox Research Centre Europe (XRCE). It is here that the author stumbles through the ups and downs of a life led in the pursuit of a better world for all (except cats). Because Romans chapter 12 verse 16 tells us to "... not be proud, but be willing to associate with people of low position", we study machine learning so that we may one day replace the people of low position with machines.
In my infinitely high view of myself, I imagine that in your daily lives you are constantly attempting to explain to your friends and colleagues what it is that I, the author, does at such a place as XRCE (because they are no doubt asking you!). To make life easier for you (the core mantra at our centre), and because docendo disco, scribendo cogito, I will proceed to attempt to explain some of the basics of one of the areas of study that I subscribe to, which is -- as noted above -- the field of machine learning (ML).
The most concise definition of the area is that ML consists of creating machines (systems, software, whatever) that can learn from data (makes sense, no?). Wow it's a huge subject. There's probably at least 70 jillion papers that fall under this area so where does one begin? Well, how about supervised learning? Here, the goal is to create a system that can predict future outcomes based on learning by example and then generalizing. At its simplest, this is basic regression.
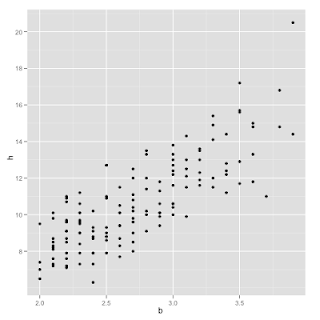
Say we have a bunch of data pairs (x,y) where x is the body weight of a domestic cat in kg and y is the weight of its heart in grams (gah! cats!!!!). By giving our system a bunch of these examples, we want it to generalize (learn) from what it sees and then be able to predict the expected weight of its heart given its body weight. So, we want to learn a function h(x) such that when we input some x (body weight) it outputs some y (heart weight). The data looks like this:
So, it looks like the relationship between body weight (along the horizontal axis) and heart weight (the vertical axis) is linear. That is, we should be able to use a linear function to predict heart weight given body weight. Because the relationship seems to be linear, we can say that our predictor h(x) = xTw = sum over the components in x times the components in w where w is a vector of parameters (this is what the algorithm will learn).
For complex machine learning problems, one of the most important issues is representation. We need a way to represent the data in a way that the computer can understand it and the data from this representation that are used to learn are called features. For this simple problem, there is only a single feature: the body weight of the (most likely evil) cat. For applications such as text classification, where we want to classify documents into categories, the features are often "bags of words". This means that each document is represented as counts of words. The short document "Hello how are you doing? I am doing fine." would be represented as follows:
Hello:1, how:1, are:1, you:1, doing:2, I:1, am:1, fine:1.
In this representation, the size of the feature space is the total number of words in the vocabulary.
Back to the simple problem above, although there is only a single feature, we also always add an 'imaginary' feature that is equal to 1 so that the learned predictor line can have an intercept other than 0; this is called the bias. So, we have x0*w0 + x1*w1 = y where x0 = 1 and we want to learn w = (w0, w1) from the data.
Since we have some existing example (or "training") data, we know that our function that we learn, for each x, should be close to its corresponding y. To do this, we need to decide on some loss function that we want to minimize over the training data. There are many of these and they have reasons for being chosen but for now we'll choose the following:
L(w) = (1/2) sum over all training examples (x(i)Tw - y(i))2 where the (i) superscripts denote each of the training examples that we have. This is called the least squares loss function because we are going to minimize (with respect to the parameters) the squared error between our prediction and the correct answer for each of the training examples.
So, how do we minimize the loss with respect to w? If you remember basic calculus, you know that if you take the derivative of a function you will get -- in a sense -- the "direction" it's going and you can follow that direction until you reach the minimum. So, this is called the gradient descent algorithm because you're descending to the minimum by following the gradient. We learn the weights iteratively by going through the data and adjusting them in the direction of the gradient as follows:
wj ← wj + η (d/dw)L(w)
where η is the learning rate. It decides how far we go with each step towards the minimum. If this is too big then we might go to far, passing the minimum on each step, and never arriving. If it's too small, it might take forever to get there because we're only getting infinitesimally closer each time.
So, what is the partial derivative of the loss function L(w) with respect to w? It turns out to be: (y(i) - x(i)Tw)x(i). So our final update in passing through the data is:
wj ← wj + η (y(i) - x(i)Tw)x(i)
This makes intuitive sense. Each time we look at an example and a feature, we alter the parameter by the amount that it was wrong. If y (the correct answer) was 5 and our prediction (x(i)Tw) was 10, then we predicted too much and the amount in the brackets will be -5. We will therefore decrement that parameter proportionally to -5. If they are very close, then we only need to make a very small update. If they are the exact same, then the update is 0 because we're at a perfect value.
There are different ways to perform these updates but one of them is called stochastic gradient descent and in this version we make updates to each of the parameter values one at a time for each datapoint. This has advantages for very large datasets (one problem is that you would never reach a perfect minimum if you don't employ a decreasing step size -- you would just jump around the minimum.. but for many problems even with a static step size you can do quite well).
Running this algorithm, we get the following parameter values:
w0 = -0.3567
w1 = 4.0341
That means, if we had a cat with body weight x=2.6kg, we would predict a heart weight of y = h(2.6) = -0.3567 + (2.6)(4.0341) = 10.13196 g. Here is that point (red) and the general predictor (blue) shown with the original training data:
Ta-da! Isn't that grand?
I was going to cover binary classification next (given some input x, predict whether it fits in the class NO (y=-1) or YES (y=1) where a common real-world example [where the e-mails are represented with the bag-of-words representation] is to tag e-mails as either SPAM or NOT-SPAM) but (believe it or not) this thing took me all afternoon on a Saturday. Maybe next time!!!
I'll leave you with a picture of my favourite twin-city of St. Donat, Quebec, Lans-en-Vercors:



No comments:
Post a Comment